Ring Buffer

A ring buffer, or circular queue, is my favorite data structure. I’ve used it countless times throughout my career to solve a myriad of things. Today i’m going to take you through an example problem, the design of a ring buffer, and an implementation (in Go).

Problem

You’re tasked with getting data from thousands of low-powered sensors to a database. You realize that maintaining connections for each sensor to the database is not a good architectural decision. Additionally, hitting the database with an insert for every sensor read will strain the backend. Thus, you want to create a co-located emitter that can receive sensor data and emit it in batches every 30 seconds to the database.

Situations like this often require consideration around:

1. What should our max batch size be?
2. What should we do if sensor data enters when the batch size is reached?
   1. Can be caused by a database connection issue, outage, or sensors emitting to much data.

While this condition is unideal, there’s a commonly taken trade-off here. Rather than trying to deal with backpressure, it may be best to just drop the oldest data stored in the emitter and ensure whatever is queued up for the next emit is the newest. This way, while there’s data loss, we can ensure we have the most up-to-date signal from the sensors.

To solve the above, we’ll design and implement ring buffer.

Buffer Design

In its simplest form, this buffer is essentially an array where the index (length(array)-1) + 1 = array[0]. Or:

$$ array = a_1, a_2, \ldots a_{n} \newline a_{n+1}=a_{1} $$

Notation aside, this creates a circle (conceptually) out of the array. Wikipedia has an excellent graphic:

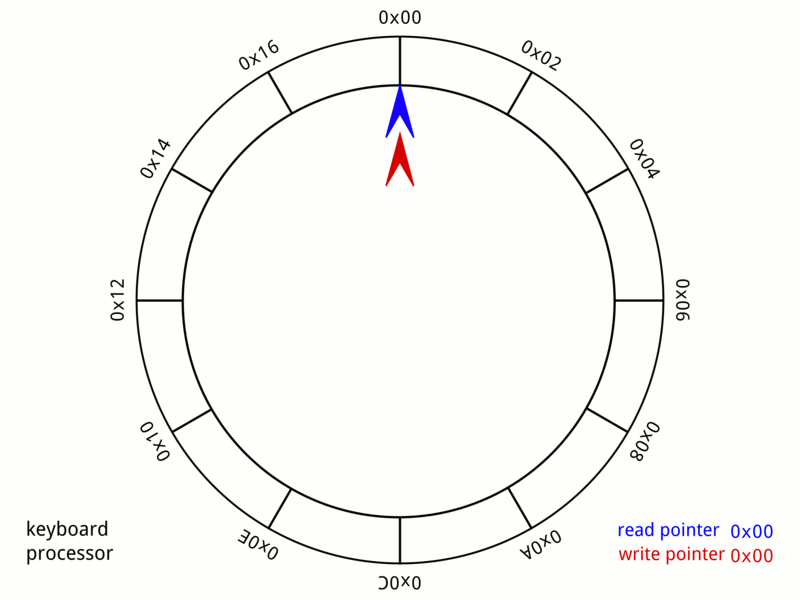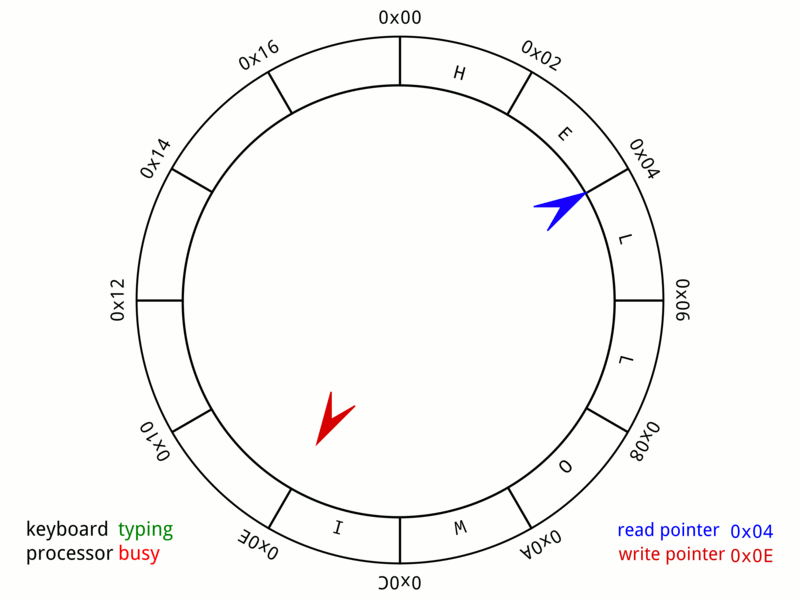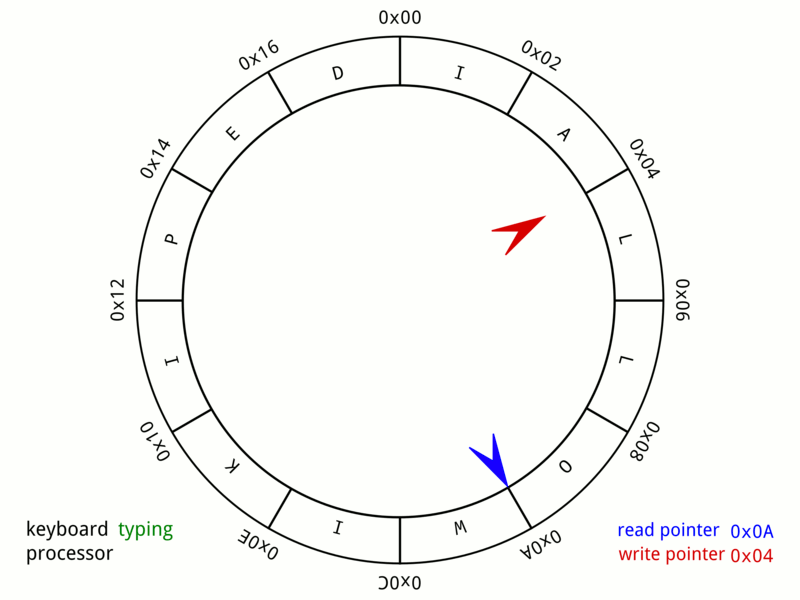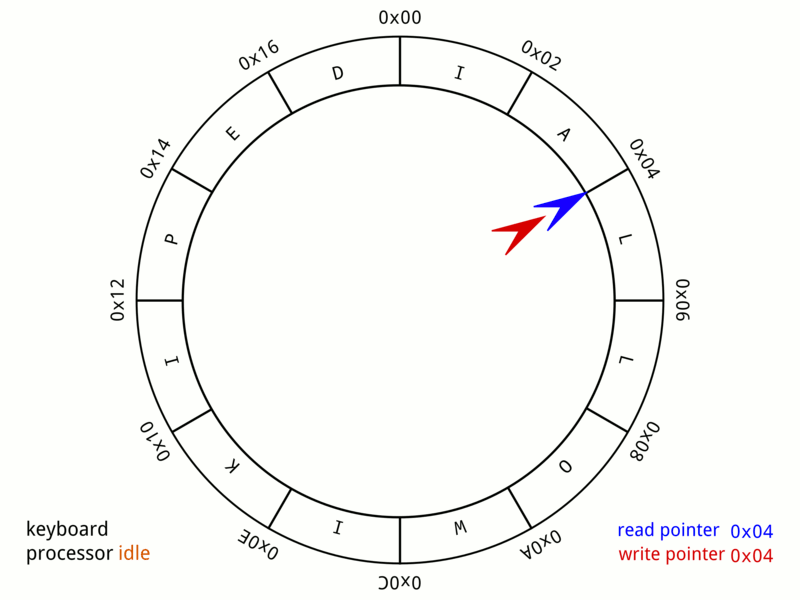
While this representation is true to our future implementation, there are a few key things to point out:

• Our read (emit) will (eventually) be triggered by time.
• We’ll allow overwriting should the write pointer reach, or pass, the read pointer.

With the conceptual idea of this data structure in place, lets build it.

Implementation

Throughout this section I’ll show snippets of code for brevity. To see the entire implementation visit https://github.com/joshrosso/ringbuffer.

First, we’ll start off with the data structure:

// RingBuffer is a circular buffer for storing [Data].
// It allows for writing and emitting data. When the
// buffer is full, the oldest data is overwritten.
type RingBuffer struct {
	data []*Data
	// total size of buffer
	size int
	// last element that was writtent to in buffer
	lastInsert int
	// next element to read during emit
	nextRead int
	// time between emit cycles
	emitTime time.Time
}

// Data represents input received from sensors.
type Data struct {
	Stamp time.Time
	Value string
}

Next a constructor for RingBuffer.

func NewRingBuffer(size int) *RingBuffer {
	return &RingBuffer{
		data: make([]*Data, size),
		size: size,
		// initialize to -1 so that we can discern when
		// no insert has occured.
		lastInsert: -1,
	}
}

Note that data gets initialized to the exact size for the buffer. This ensures there is no overhead in Go needing to reallocate arrays as the slice grows.

Next let’s create an API for inserting to the ring buffer.

// Insert adds a new [Data] to the [RingBuffer].
// If the buffer is full, the oldest data is overwritten.
func (r *RingBuffer) Insert(input Data) {
	r.lastInsert = (r.lastInsert + 1) % r.size
	r.data[r.lastInsert] = &input

	if r.nextRead == r.lastInsert {
		r.nextRead = (r.nextRead + 1) % r.size
	}
}

There’s a bit of cleverness here with expressions like (r.lastInsert + 1) % r.size. This expression enabled us to move forward in the buffer, ensuring that if we’re at the end of the array, we start at the beginning. To make the example concrete, consider an array of size 5 where we want to move to the "next" element from index 4:

$$ nextIndex = ((4 + 1)\mod 5) = 0 $$

With insert in place, we can now implement the emit functionality.

// Emit returns all data in [RingBuffer] since the last call
// to Emit.  If no data has been written since the last call
// to Emit, an empty slice is returned.
func (r *RingBuffer) Emit() []*Data {
	output := []*Data{}
	for {
		if r.data[r.nextRead] != nil {
			output = append(output, r.data[r.nextRead])
			r.data[r.nextRead] = nil
		}
		if r.nextRead == r.lastInsert || r.lastInsert == -1 {
			break
		}
		r.nextRead = (r.nextRead + 1) % r.size
	}
	return output
}

As a final step, you can setup main such that it validates the buffer behavior.

func main() {
	rb := NewRingBuffer(5)
	currentRune := 'a' - 1
	fmt.Println("EMPTY TEST:")
	spew.Dump(rb.Emit())
	fmt.Println("FULL TEST:")
	for i := 0; i < 10; i++ {
		currentRune++
		rb.Insert(Data{
			Stamp: time.Now(),
			Value: string(currentRune),
		})
	}
	spew.Dump(rb.Emit())
}

In the 2 tests above, the EMPTY TEST will return an empty slice and FULL TEST will return f, g, h, i k.

EMPTY TEST:
([]*main.Data) {
}

FULL TEST:
([]*main.Data) (len=5 cap=8) {
 (*main.Data)(0xc000108540)({
  Stamp: (time.Time) 2023-03-24 07:07:11.779010999 -0600 MDT m=+0.000126421,
  Value: (string) (len=1) "f"
 }),
 (*main.Data)(0xc000108570)({
  Stamp: (time.Time) 2023-03-24 07:07:11.77901113 -0600 MDT m=+0.000126550,
  Value: (string) (len=1) "g"
 }),
 (*main.Data)(0xc0001085a0)({
  Stamp: (time.Time) 2023-03-24 07:07:11.779011261 -0600 MDT m=+0.000126684,
  Value: (string) (len=1) "h"
 }),
 (*main.Data)(0xc0001085d0)({
  Stamp: (time.Time) 2023-03-24 07:07:11.779011404 -0600 MDT m=+0.000126826,
  Value: (string) (len=1) "i"
 }),
 (*main.Data)(0xc000108600)({
  Stamp: (time.Time) 2023-03-24 07:07:11.779011556 -0600 MDT m=+0.000126978,
  Value: (string) (len=1) "j"
 })
}

In the case of FULL TEST, a through j are inserted into the ring buffer, but since the size is set to 5, a through e are overwritten and when emit is called, f through j is all that remains.

Now that we’ve got functionality validated around the buffer, the final step you’d setup is to create a Run() function that can be called in a separate Go routine. You can use the emitTime property setup in the RingBuffer struct to configure a loop using time.Sleep. Note that if you go this extra step, it becomes extra important you consider a mutex that can lock the buffer during an emit cycle!

Wrapping up this exercise, there are a few items of note.

• You should consider needs around thread safety. It’s not handled here in order to keep the code samples succinct, but mutex’s when doing emit and potentially even insert should be considered.
• If you find expression like (r.nextRead + 1) % r.size ugly, one way to clean it up would be to introduce a new type for lastInsert and nextRead that holds an int and has a method for Next(), this would abstract the idea of wrapping around the data structure.
• In Emit, we set the Data read to nil. This could trigger some garbage collection prematurely, however I think this keeps the state of the data structure clean and is an optimization that won’t see significant benefit in most cases.
• Go has a ring package, but I’m not too crazy about its API and its implemented as a linked list, which is likely to have lesser performance since its non-contiguous memory.

Closing

One of the beauties of data structures is that we can solve so many problems adding a little sugar on top of an array or map (hash table). This small implementation can solve some real-world problems and is a great tool to have in the belt. I also love some of the tricks like using modulo to ensure we end up back at index 1 if we’re trying to get the next element at the end of the array. Simply put, I find it really weirdly inspiring knowing simple solutions with known primitives are often just sitting amongst us waiting to be used 🙂. Hope you found this interesting and happy building!